1ランク上の品質、コストを実現する幾何公差の逆転活用法 第3回 基準編 「データムの使い方を身につける」
技術士の折川先生による連載「1ランク上の品質、コストを実現する幾何公差の逆転活用法」です。第3回は基準編 「データムの使い方を身につける」です。
目次
はじめに
前回までに、設計意図を正しく伝達し、機能品質やコストを適正化するための、幾何公差の有効的な活用法を紹介した。
今回は、この幾何公差を使う上で、最も基本的で重要な要素であるデータムを取り上げ、その意義や使い方について解説する。
なお、文中、理論的に正確な寸法をTEDと略記している。
1. 基準としてのデータム
1-1. 基準とは
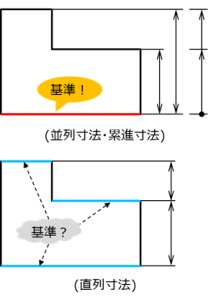
図 1 基準の解釈例
「基準」の一般的な定義をあげると、以下のようなものになる。
・部品の寸法指示の開始位置 (設計基準)
・加工の開始位置 (加工基準)
・測定の開始位置 (測定基準)
最終的に、製品を組み上げる際は、構成部品の固定や位置決めとして使用される。
そのため、どこが基準であるかを、加工や検査、組立工程に正しく伝える必要がある。
図1に、代表的な寸法記入例と基準の解釈を示す。
図上は並列寸法や累進寸法で指示したもので、この場合は寸法の開始点が一見して理解でき、この図例では底面が基準である、と判断しても特に問題はない。
一方、図下の直列寸法指示の場合は、どの面が基準であるかが不明である。
この場合、通常は、図面内に基準とする線であることを注記や記号(”基準線”、”Datum”、”D.L“など)で明示することになる。
1-2. データムとは
「データム」の一般的な定義は、他の形体の状態を定義するための基準となる形体のことである。
ここで形体とは、部品上の点、線、面(Feature)を指し、状態とは、それらの位置や姿勢(傾き)を指す。
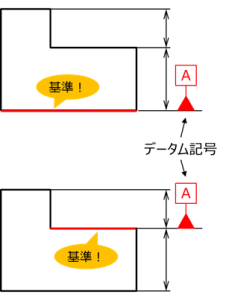
図 2 データムによる基準指示例
図2にデータムの使用例を示す。
どちらも直列寸法の図であるが、図上は底面に、図下は中間の面にデータムを指定している。
このように、データムを使うことで、この部品のどこが基準であるかを明示できる。
重要なのは、データムが、基準を指示する世界共通の記号である、という点である。

図 3 データム記号
図3にデータム記号の書き方例を示す。
一般的には、データムは黒ベタの正三角形と四角枠で囲った英大文字の組み合せで表記する。
また、図面を正面から見た場合に、データムの文字がその外枠も含めて正立しているように記入する。
1-3. データムの指示例
図4に代表的なデータムの指示例を示す。
表面への指示か中心線/面への指示かで呼び方は異なるが、後者の場合は、図のように寸法線の延長方向にデータム記号を合わせることに注意する。
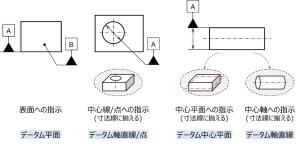
図 4 データムの指示例
1-4. データムによる自由度の拘束
物体にはx,y,zの3軸の並進方向と回転方向の、合わせて6つの自由度がある。
データムは、これらの自由度の全部または一部を拘束して対象部品を固定できるように設定する。
そして、このデータムを参照した幾何公差を用いて、部品上の形体(面、中心線など)の位置や姿勢を規制する。
図5は、データムによる自由度の拘束の一例である。
同図左の、3平面へのデータム指定による拘束が最も基本的なものであるが、実務的には同図中央または右のような拘束方法をとることが多い。

図 5 データムによる自由度の拘束例
なお、注意しなければならないのは、データムは必ずそれを参照する幾何公差とセットで使用される、という点である。
データムは、幾何公差による形体の規制の基準であり、どの幾何公差にも参照されず、単に自由度の拘束のためだけに単独で図中に存在することはない。
2. データム形体と実用データム形体
2-1. 図示上のデータムと実際のデータムの違い
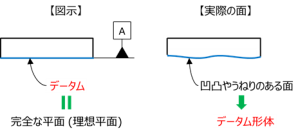
図 6 データムとデータム形体
データムで指示された面は、図面やCAD上では完全な平面だが、加工後の実際の面は、程度の差こそあれ、必ず凹凸やうねりがある。
このデータム指示された加工物の面のことをデータム形体(Datum feature)と呼ぶ。(図6参照)
2-2. データムの代用
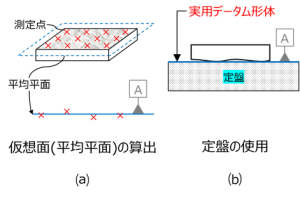
図 7 実用データム形体
実際の面すなわちデータム形体は、そのままでは測定の基準として扱うには相応しくないため、これを理想平面に近似することを考える。
図7⒜はデータム形体上の多数の点の座標を3次元測定機などで取得し、平均平面を算出する方法で、同図⒝は対象物を定盤のような、面が精度よく仕上がった台の上に置き、その面を基準とする方法を示したものである。
⒝のように、データム形体を実体で代用したもののことを実用データム形体(Simulated datum feature)と呼ぶ。
データム形体と実用データム形体は、言葉が似ているため区別しにくいが、これをわかりやすく説明した絵が市販書籍にあるので紹介する。
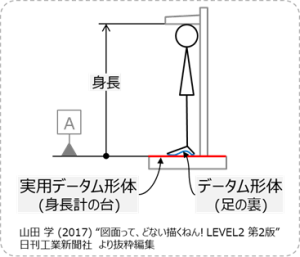
図 8 データム形体と実用データム形体
図8は身長を測っている様子を示したもので、身長計で実際に測っているのは身長計の台の上から横規(頭上の板)までの距離である。
つまり、凹凸のある足の裏がデータム形体で、これを代用した身長計の台の上が実用データム形体となる。
3. データムの優先順位と設計意図
3-1. 組み付け順の検討
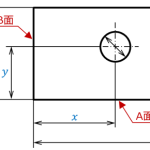
図 9 サイズ公差指示図面
図9に示す部品の、相手部品への組み付け方法を検討する。
ここで、底面をA面とし、左側面をB面とする。
丸穴の中心までの距離は各面からx, yである。(x, yには適切な公差指示がなされているものとする)
この図例は従来記法による図面であることに留意する。
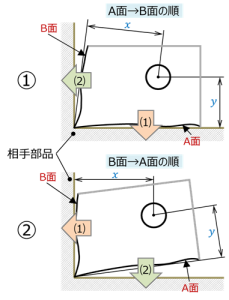
図 10 組み付け順の比較1
図10は、この部品をL字形の相手部品に組み付ける手順を考えたものである。
同図上①は、部品のA面を最初に相手部品に突き当て、次にB面を突き当てている。
一方同図下②は、逆にB面を先に突き当て、A面を後から突き当てている。
ここで注目したいのは、組み付けが終わった後での、相手部品から見た丸穴の位置である。
前回説明したように、サイズ公差指示の場合、この丸穴の中心の位置までの距離は2点間測定で評価される。
図10ではわかりやすいようにA面とB面の間にあえて大きな角度を付けてあるが、丸穴中心の位置は、この図に示すように実際に仕上がった面からの距離である。
この距離、x, yの値が許容限界サイズ内に入っていれば部品としては合格品であるが、相手部品に組み付けた状態では、どちらの面を先に突き当てるかで丸穴の位置が異なる。
例えば、相手部品側に、丸穴に相当する位置に軸が配置されているとした場合、①と②でその軸が穴に挿入できず、組み付け不良が発生する可能性がある。
3-2. 組み付け順の明示
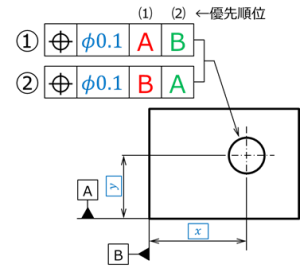
図 11 幾何公差指示図面
図11は図10の部品の穴位置に対して位置度を指定した例である。
前項でA面、B面とした面には各々データムA,データムBを設定し、この2つのデータムを参照して①と②の2種類の位置度指示が与えられている。
両者の違いは幾何公差記入枠内でのデータム記号の並び順である。
データム記号が複数並ぶ場合は左側にあるものほど優先順位が高いため、①はデータムAが第1優先、Bが第2優先となり、②はその逆順となる。
穴位置はTEDを使って寸法指示している。
では、この図面によって作製された部品を先ほどと同じL字形の相手部品に組み付ける手順を考えてみる。
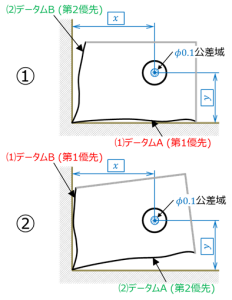
図 12 組み付け順の比較2
図12上の①は最初に第1優先であるデータムA面を相手部品に突き当て、次に第2優先のデータムB面を突き当てた状態で、同図下の②はその逆順で突き当てた状態である。
この部品は幾何公差によって、穴の中心がTEDで指定されたx, yの理想的な位置を中心とする、Φ0.1の円筒公差域内にあることを指示されている。
この図例も、わかりやすいように形状を極端にゆがめて描いてあるが、部品単体での穴位置は異なるが組み付けた状態ではどちらの場合も相手部品に対する位置関係は同じとなっていることがわかる。
つまり、前の例のように、相手部品側に軸が立っているとすると、この部品の穴と相手の軸は理屈上は必ず嵌合が成立する。(但し、相手部品の軸も同様に位置度による幾何公差指示がなされている必要がある)
例えば、設計者が①を選択した場合、加工者も測定者も製造担当も、図面からその意図を読み取って、データムAを第1基準とした作業をすることになる。
この例からわかるように、設計段階でデータムの優先順位を明記しておくことで、組み付けに至るまでのプロセス全体に設計意図を伝えることができる。
3-3. 設計意図との関係
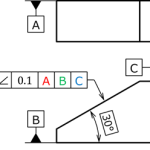
図 13 斜面を持つ部品
データムの優先順位に関する最後の例として、図13に示すくさび形の部品をとり上げる。
この部品の斜面には傾斜度が指定され、データムはA,B,Cの順で記入されている。
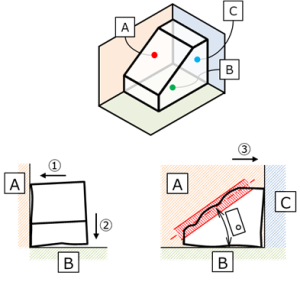
図 14 組み付け順と斜面の評価
従って、この傾斜度指示は、部品が相手部品に対してA→B→Cの順番で組み付けられることを、設計意図として表現している。
図14に示したように、この部品は、A、B、C各面を相手部品に突き当てた後で、その斜面が、傾斜度の角度基準となっている、データムBの面から30°の角度の指定公差域に入っているかどうかが評価される。
評価されるのは斜面の位置であるが、そのための部品の位置決めの順番が重要であり、それを幾何公差記入枠内のデータムの並び順で決めている、ということに注意する。
4. 共通データム
4-1. 共通データムとは
 2つの異なる形体(表面や中心線など)へのデータムを、一組のデータムとして扱った時のデータムのペアを共通データムと言う。
2つの異なる形体(表面や中心線など)へのデータムを、一組のデータムとして扱った時のデータムのペアを共通データムと言う。
幾何公差記入枠内での表記方法は右図のように、1つのデータム枠(左から3番目以降の枠)の中に、ペアとするデータム記号をハイフンでつないで記入する。
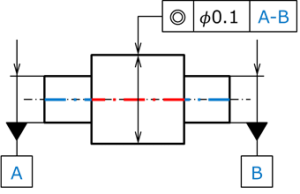
図 15 共通データムの代表的使用例
図15に代表的な使用例を示す。
段付き軸に対する共通データムの図示例は、JIS規格ほか種々の専門書でも紹介されている。
この図では、左側の小径軸にデータムA、右側にデータムBが設定されており、それらを共通データムとした同軸度が、中央の大径軸の中心線に指示されている。
この意味は、左右の小径の軸の中心線2本を1本のデータム軸直線として扱い、それを参照して中央の大径の軸の同軸度を規制する、ということである。
ここで注意すべきことは、共通データムに指定された2つのデータムの間には優先順位がない、という点である。
A,B2つのデータム記号が、前節で述べたように、幾何公差記入枠の別々のデータム枠に入っていれば、並び順による優先順位が発生するが、一つのデータム枠に入っている場合は順位は関係ない。
4-2. 共通データムの適用例1
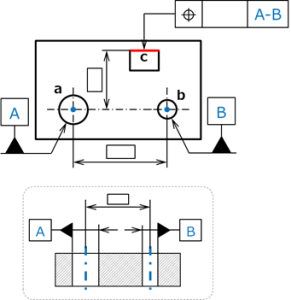
図 16 平行2軸
図16は平行な2本の穴の中心線に対して共通データムを指示した例である。
2つのデータムA,Bは、cで示した面の垂直方向の位置を決めるために、その基準となる水平線を定義するために使用されている。 従って優先順位を考慮する必要がないため、共通データムとしてある。
面cの位置度の評価に用いられるのは、穴aと穴bの中心線を通る仮想面からの距離である。
なおこの図例では、穴間の距離に対してTEDを指示しているが、穴間ピッチのばらつきも含めた位置度規制をしている、と解釈する。
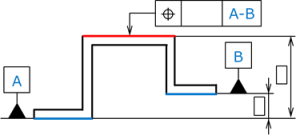
図 17 平行2平面
図17は高さの異なる平行2平面に対して共通データムを指示した例である。
2つのデータムA,Bを設定した平面はどちらの面を先に相手部品に取り付けるかは不問であるため、これらを共通データムとしてある。
この例では、データムAとBの距離寸法がTEDになっている点に注意する。
4-3. 共通データムの適用例2
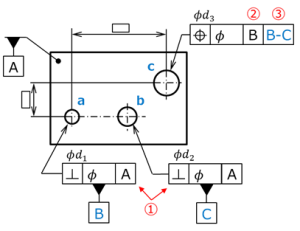
図 18 平行円孔の組み合せ
図18は平行な2つの穴a, bを参照して、穴cの位置を規制している例である。
この図例の解釈は以下となる。
① 穴 a, bへのデータム指示は、データムAに対する直角度のみ要求している。
② 第1優先データムBは穴aを原点としていることを示す。
③ 共通データムB-Cはaとbを結ぶ直線を水平基準としてしていることを示す。
結果として、穴cはデータムBを原点とし、データムB-Cで決まる水平(x)基準からなるxy座標系により、位置が規制されていることになる。
本例のような共通データムの使い方はあまりなじみがない方もいるかもしれないが、水平や垂直の軸方向を決定するための表記方法の一つであることを、理解しておいていただきたい。
5. 形体グループとデータム
5-1. 形体グループとは

図 19 形体グループの例
形体グループ(A group of features, Feature group)は、形状が同じ複数の形体の集まりを指し、図面上で “2x○○” 等の指示がされた部位が該当する。
その例を図19に示すが、ここでは、形体個数が3以上の場合は同一円周上に等間隔で配置されたものが対象であり、同図右のような配置は対象外である。
5-2. 形体グループへのデータム指示例
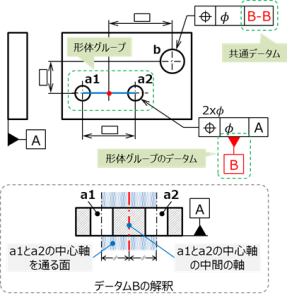
図 20 形体グループのデータム
図20に形体グループに対してデータム指示した場合の図例を示す。
穴a1とa2が同径で、この2つが形体グループとなる。
この形体グループに対して設定したデータムBが、形体グループへのデータムとなり、このデータムを参照して穴bの位置度を規制している。
この場合、約束事として、形体グループのデータムは共通データムとして扱い、同じデータム記号をハイフンでつないで記入する。
なお、データムBの解釈は同図下に示すように、2つの穴の中心線を含む平面と、その中間の軸となる。
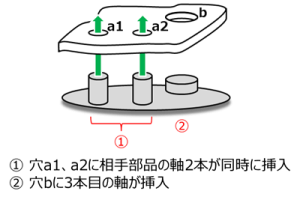
図21 形体グループと設計意図
この図例の設計意図を図21に示す。
この部品の穴a1、a2には相手部品の2本の軸が同時に、すなわち順番は関係なく挿入され、それらの軸をガイドとして、穴bに相手部品の3本目の軸が挿入される、という構造である。
実場面での登場頻度は低いかもしれないが、このデータムの使い方も理解しておいた方がよい。
まとめ
データムは、幾何公差の参照基準を明確にするための、重要な要素である。
データムの優先順位を適切に設定することで、設計意図を加工や検査、組立工程の現場に正しく伝達することが可能となる。
共通データムや形体グループへのデータムの活用法を理解することで、幾何公差による設計意図の表現がより強力になる。
今回解説した、データムの考え方や活用法を身につけ、幾何公差設計を更に有意なものとしていただきたい。
次回は、幾何公差を使用する上での、よくある間違いや作法上の注意点について解説する。
|
折川技術士事務所 代表 〔略歴〕 |
 |


