機械設計者の基礎知識4力学に触れよう 第一回 ベアリングにかかる負荷
今回より、技術士の春山先生に、設計者の方へ向け材料力学・機械力学・熱力学・流体力学の「4力」について問題を解きながら解説いただく連載をスタートします。
第一回は材料力学についてです。一度学んだ方も振り返りのためや実例に活かしていただけるポイントを解説していますので、ぜひご覧ください。
はじめに
 機械設計を行う際、いくつかの機械要素を選定することがあります。この機械要素を選定するにあたっては、いくつかの力学の知識が必要となることがあります。
機械設計を行う際、いくつかの機械要素を選定することがあります。この機械要素を選定するにあたっては、いくつかの力学の知識が必要となることがあります。
例えばベアリング(軸受)を選定するにあたってはそのベアリングにかかる負荷を計算する必要があります。図のような使い方をする場合、軸が受ける負荷wからベアリングに生じる反力R1およびR2を求めます。これは材料力学におけるはりの問題です。
本来、機械設計を行う者には基礎的な力学知識が必須なのです。
ベアリングにかかる負荷を計算しよう。(材料力学)
 図2に示すように両端を軸受で保持し、ワークを受ける軸を設計します。
図2に示すように両端を軸受で保持し、ワークを受ける軸を設計します。
これはまさしく図1のような等分布荷重を受ける軸であり両端の軸受けには反力が発生しています。
これは材料力学でいう等分布荷重を受ける両端支持の梁(はり)の問題です。
このとき両端の支持部に発生する反力R(=R1=R2)は次の式で与えられます。
![]()
[計算例]
・条件
ワーク質量 M:100[kg]
軸受間寸法 L:200[mm]
このときの反力を求めます。
まずは等分布荷重を求めます。ワーク質量が100kgのため、重力加速度g=9.8として、軸には100×g=100×9.8=980[N]の力がかかっています。これが軸の長さL=200にわたり作用するため等分布荷重は次の通りになります。
![]()
よって求める反力は次の通りになります。
![]()
[補足]
材料力学の教科書などでは等分布荷重が与えられていてそこから反力やたわみを計算する問題が出ます。しかし実際の設計では等分布荷重ではなく、作用する質量(質量[kg]であり力[N]ですらない)が条件としてあって検討を進めることも多々あります。その場合、今回の問題のように質量から等分布荷重を求めてもいいのですが、質量M[kg]・長さL[mm]・等分布荷重W0[N/mm]の関係を使った方が早いです。
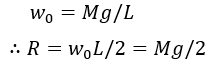
[補足終わり]
上記計算例のように材料力学におけるはりの問題として、軸受にかかる反力を求めます。このようなはりの公式は材料力学の教科書はもちろん、インターネットで「はりの強度計算」と検索をすればたくさん出てきます。さらには条件を入力すれば自動で計算してくれるサイトもあります。しかし、それだけでは落とし穴にはまることがあります。
例えば今回の計算例では今のところ反力R=490[N]となっていますが、これは正しくありません。正確にはこれに加えて、軸自身の重さによる力が発生しています。
つまりワークの質量により発生する反力と軸の自重による反力を合わせたものがベアリングに発生している反力ということになります。
[重ね合わせの原理]
はりに異なる2つの荷重AとBが作用しているときに発生する反力や変形量は、荷重Aが単体で作用しているとして求めたものと、荷重Bが単体で作用しているとして求めたものとを足し合わせたものとなります。(重ね合わせの原理)
図3に示すように軸の直径をdとして、その密度をρ[kg/mm3]とします。
[計算例]

・条件
軸直径 d:20[mm]
材質 S45Cとする。
密度 ρ:7.84 × 10⁻⁶ [kg/mm3]
軸質量M’から軸質量により発生する等分布荷重W’0、さらには反力R’を求めます。
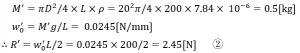
よって正確には、軸受に発生する反力Rallは①②を足し合わせて492.45Nとなります。
[例題]
図4に示すように軸の左端からL1の位置にP[kg]の質量を受けています。
次の条件の下で軸受に生じる反力R1、R2を求めてください。
・条件

質量 P:100[kg]
軸受間寸法 L:200[mm]
質量位置 L1:150[mm]
軸直径 d:20[mm]
材質 S45Cとする。
密度 ρ:7.84 × 10-6 [kg/mm3]
・計算式
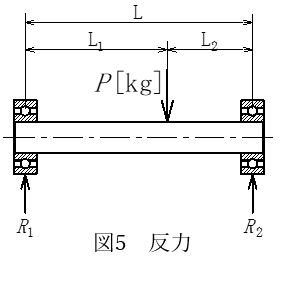
集中荷重W[N]を受ける単純支持はりの支点に生じる反力は次の通りです。
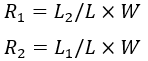
*重力加速度をg(=9.8[m/s²])として、集中荷重は
W[N]=9.8Pとなります。
・解答
質量100kgにより生じる反力
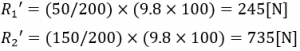
軸質量M’から軸質量により発生する等分布荷重W’0、さらには反力R’を求めます。
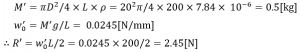
よって
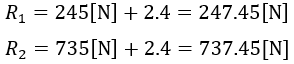
[チャレンジ]
はりの応用問題です。集中荷重を受ける単純支持梁のたわみ量の計算式を用いて解いていきます。解答はウェビナーで行います。
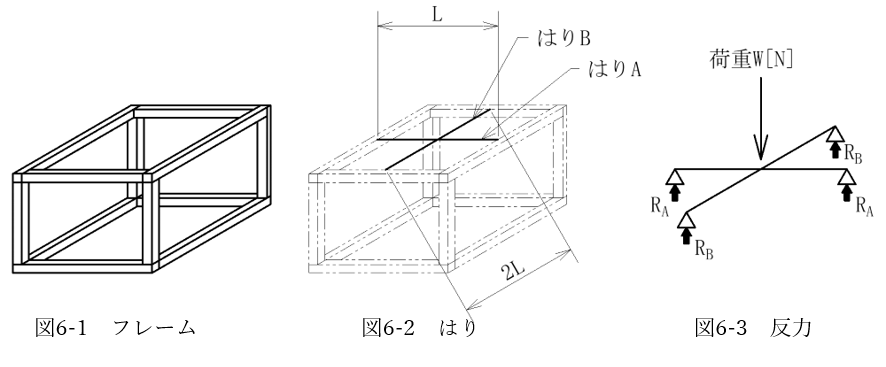
問題
図6-1に示すようなフレームがあります。
図6-2に示すように、このフレームの天面中心を通るようにはりAとBを入れます。はりAの長さはL、はりBの長さは2Lであり、はりAとはりBとは互いの中心で交わります。
図6-3に示すように、いまこの交点に荷重W [N]が作用します。このときはりA,Bそれぞれの支点に生じる反力RAとRBを求めてください。
ただしはりの自重は無視できるものとし、フレーム自体は剛体(変形しない)、フレームとはりとの交点=単純支持(ピン結合)としてください。
また、はりの断面二次モーメントをI、断面係数をz、ヤング率をEとします。
[参考]集中荷重を受ける両端単純支持はり
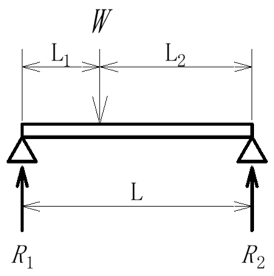
・反力
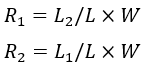
・最大曲げモーメント(作用点で発生)
![]()
・最大たわみ