機械設計者の基礎知識4力学に触れよう。 第3回　熱応力と伝熱

本連載では、技術士の春山先生に、設計者の方へ向け材料力学・機械力学・熱力学・流体力学の「4力」について解説いただいています。実務で使用できる例題をご用意しているため、日々の業務に取り入れやすい内容です。

第三回は熱力学について、熱応力と熱伝の例題をそれぞれ解説します。

 

はじめに

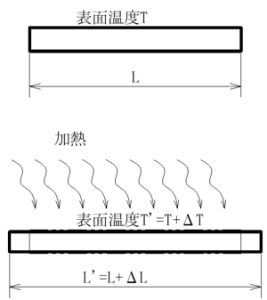機械はそれ自体が発熱することもあれば、何らかの目的をもって加熱するものもあります。ある物質が加熱あるいは冷却されたとき、もともと温度Tだったものに温度変化ΔTが生じてT’＝T＋ΔTになります。さらにこの温度変化に比例してそのサイズもLからΔL変化してL‘＝L+ΔLになります。このサイズ変化は材料力学、加熱や冷却による熱の移動は熱力学の基礎になります。

本来、機械設計を行う者には基礎的な力学知識が必須なのです。

 

 

 

 

［１］熱により発生する熱応力を計算してみよう。

（１）熱CVD装置

図1.1に示すような熱CVD（Chemical Vapor Deposition）装置を考えます。

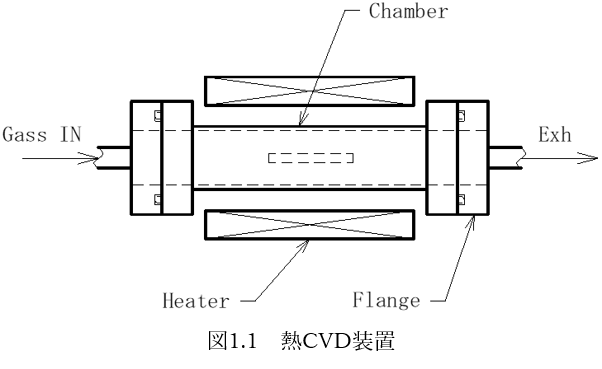
チャンバー内に触媒を入れてフランジで密封・固定します。内部にガスを流し加熱することで触媒とガスを熱反応させて目的の生成物を得ます。

はじめにで述べたように加熱されると物体、この場合はチャンバーが伸びようとします。しかしこのチャンバーは両端をフランジで固定されているため伸びることができません。

逆の見方をすると全体が加熱された状態にあるとき、図1.2（b）に示すようにチャンバーの全長はL‘まで伸びるはずですが、図1.2（c）に示すようにフランジにより圧縮されてLになっていると言えます。

 

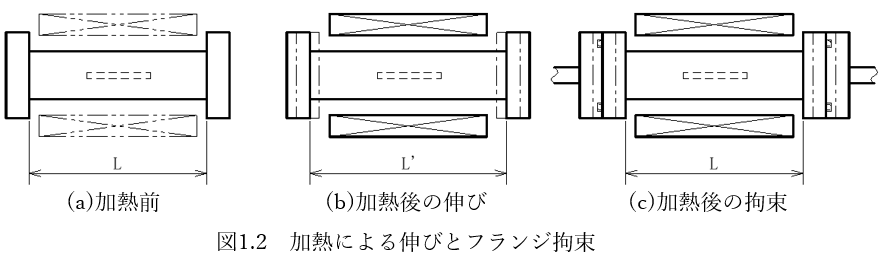
このときチャンバー自身には圧縮されることにより内部圧縮応力が発生しています。このように熱により発生する応力を特に熱応力と呼びます。材料や形状によってはこの熱応力によって思わぬトラブルが発生しかねません。

それではこの熱応力の計算について見ていきたいと思います。

 

［条件］

材料　合成石英ガラス

L＝600mm

加熱前温度　T= 20℃（室温）

加熱後温度　T=800℃

 

 

（2）解説

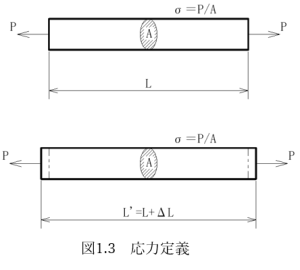図1.2に示すように、断面積A［mm²］を持つある材料が引張力、あるいは圧縮力P［N］を受けたときの応力σ［N/mm²］は次式で定義されます。

 

σ=P/A                               （ⅰ）

ここで力引張力Pを受けた長さLの材料がΔL伸びてL‘になったとします。このときひずみεを元の長さLと伸び量ΔLを用いて次のように定義します。

ε=ΔL/L                            （ⅱ）

 

材料の変化が弾性領域内^*1にある場合、応力σ［N/mm²］と材料固有のヤング率（縦弾性係数）E［N/mm²］、ひずみεには次の関係があります。

 

σ=Eε=EΔL/L               （ⅲ）

 

この（ⅲ）式をフックの法則と言います。（ⅰ）式と（ⅲ）式から引張力Ｐと材料の変化ΔＬには次の関係が成り立ちます。

 

P=AEε=AEΔL/L          （ⅳ）

（あるいは　ΔL=PL/AE）

 

（参考）SS400のヤング率　E≒206［GPa］＝2.06×10⁵［MPa］（MPa＝N/mm²）

参考Web⇒材料選定ガイドTOP｜Kabuku Connect（カブクコネクト）

 

*1　材料にある一定の力Pをかけるとその材料は変形します。次にこの一定の力Ｐを除いたときに材料は元の形状に戻ります。これを弾性変形と言います。Ｐにより発生する内部応力がある一定の値よりも大きくなると材料は元の形状に戻ることができず永久に変形してしまいます。これを塑性変形といい、塑性変形が始まる応力値を降伏点といいます。変形が弾性変形にとどまる応力の領域を弾性領域と呼びこの領域においてはフックの法則（上記（ⅲ）式の関係）が成り立ちます。塑性領域ではこの関係は成り立ちません。

 

ある材料が加熱されて温度がTからΔTだけ変化してT‘になったとき、この材料の伸びは次式で表されます。

 

ΔL=αLΔT                      （ⅴ）

 

α：線膨張係数（あるいは熱膨張係数）

（参考）SS400の線膨張係数　α=11.8×10^-6［/℃］

 

（ⅲ）式と（ⅴ）式から次式が導出されます。

 

σ= EαΔT                        （ⅵ）

 

温度変化ΔTが生じた際に両端を拘束されているなどの条件から、伸びが生じないときに応力σが発生します。このΔTとσの関係が上記（ⅵ）式になります。

この（ⅵ）式の関係から、フランジで固定されたチャンバーを加熱して温度変化を生じさせたときにチャンバーに発生する内部応力を求めることができます。

 

 

（３）解答

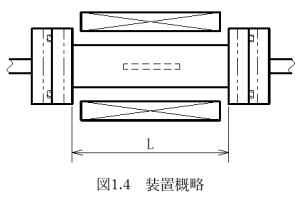［条件］図1.4に示すような熱CVD装置においてチャンバーに生じる熱応力を計算していきます。

チャンバー材料：合成石英ガラス

L＝600mm

加熱前温度　T= 20℃（室温）

加熱後温度　T=800℃

合成石英ガラスの物性値は次の通り

ヤング率        ：70［GPa］＝7.0×10⁴［MPa］

線膨張係数    ：0.58×10^-6［/℃］（@0～300℃）

圧縮強さ        ：1150［N/mm²］

 

（ⅵ）式から熱により発生する内部圧縮応力は次の通りになります。

σ= EαΔT=（7×10⁴）×（0.58×10^-6）×（800-20）

=31.67［N/mm²］

 

合成石英ガラスの圧縮強さは1150［N/mm²］であるため今回の場合、熱応力単体では特に問題ないことがわかります。

ただし、内部を加圧したり真空引きを行う場合はそれらの影響を組合わせて検討する必要があります。

 

 

 

（４）チャレンジ問題

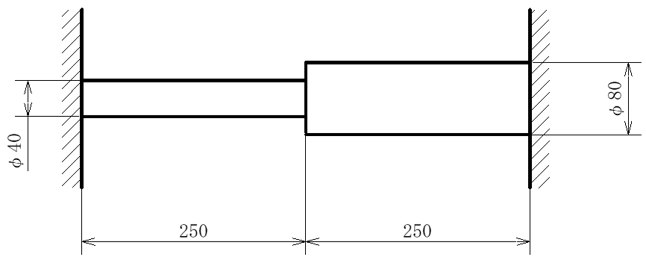
図のように段付き棒がその両端を固定されています。材料はSS400で温度が20℃から100℃に変化しました。このとき、棒の細い部分に発生する内部応力を求めてください。

SS400物性値

ヤング率             ：206GPa

線膨張係数        ：11.8×10^-6/℃

考え方

①材料の温度が20℃から100℃に変化したとき、仮に両端の拘束がない（固定されていない）とすれば細い部分はΔL1、太い部分はΔL2伸びます。

この二つを合わせて全体としてはΔL=ΔL1+ΔL2伸びます。

 

②いま問題の条件では両端が固定されているため段付き棒は伸びることができません。つまり全体としてはΔL圧縮された状態と見ることができます。このとき棒には圧縮力Pが作用することになります。

 

③圧縮力Pが作用したときの細い部分の圧縮量をΔL1‘、太い部分のそれをΔL2’とするとこの合計、つまり全体の圧縮量が前述した固定が無いと仮定したときの全体の伸びΔLに等しくなります。ΔL=ΔL1‘+ΔL2‘

（参考）圧縮力Pが作用しているときの圧縮量ΔL’=PL/AE：（ⅳ）式より

 

以上の関係から圧縮力Pを求めて、細い部分の断面積から応力値を求めます。

解答はウェビナー動画をご覧ください。

 

 

［２］伝熱の問題、室温を20℃に保つヒーターの電力を計算してみよう。

（１）部屋の中のヒーター問題

図2.1のような一辺が5mの部屋を考えます。壁および屋根の厚みは100㎜のコンクリートとします。

部屋の中にはヒーターが置かれており、外気温10℃に対し室温は20℃一定に保たれています。

このとき、ヒーターの消費電力を考えてみます。

 

このような条件の問題を熱通過と言います。伝熱の形態には2種類、すなわち熱伝達と熱伝導があります。

 

熱伝達：ある物質と流体の間の熱移動。

熱伝導：物質内部での熱移動。

 

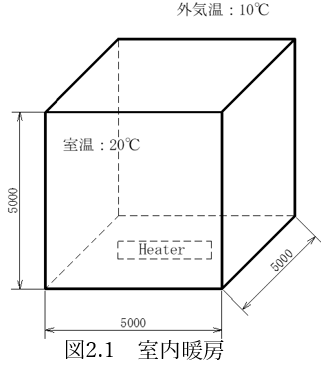図2.2に壁面を拡大したものを示します。室内空気（高温流体側）から壁内面への熱移動は熱伝達になります。壁内部の熱移動は熱伝導であり、さらに壁外面から外気（低温流体側）への熱移動は熱伝達になります。そしてこのように熱伝達と熱伝導が組み合わさったものを熱通過と呼びます。

このとき熱の通過量、熱流束q［W/m²］は次式で表されます。

\[
q= \cfrac{1}{(\cfrac{1}{h_1}+\cfrac{\delta}{\lambda}+\cfrac{1}{h_2})}(Tf1-Tf2)
\]

 

 

 

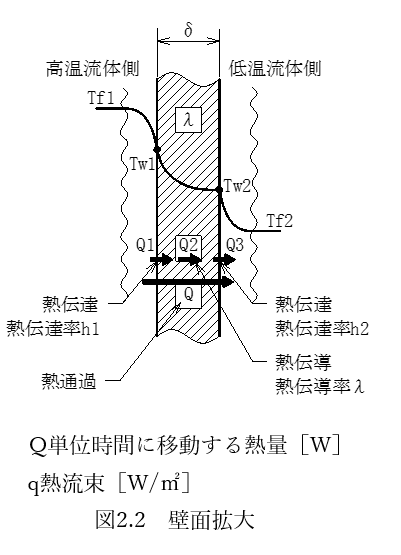
Tf1      ：高温側の流体温度

Tw1    ：高温側の壁面温度

h1        ：高温側の熱伝達係数

Tf2      ：低温側の流体温度

Tw2    ：低温側の壁面温度

h2        ：低温側の熱伝達係数

δ        ：板厚

λ        ：熱伝導率

いま、室内の熱伝達係数h1を23［W/m²K］、室外のh2を9［W/m²K］、コンクリ―ト壁の熱伝導率λを2.3［W/mK］とします。床面は断熱されているとして、ヒーターの消費電力はいくらになるでしょうか。

 

（2）解答

\[
q= \cfrac{1}{(\cfrac{1}{h_1}+\cfrac{\delta}{\lambda}+\cfrac{1}{h_2})}(Tf1-Tf2)
\]

問題から、h1=23、h2=9、λ=2.3、δ=100mm=0.1m、Tf1=20、Tf2=10　これらの値を上式に代入します。

\[
q= \cfrac{1}{(\cfrac{1}{23}+\cfrac{0.1}{2.3}+\cfrac{1}{9})}(20-10) =50.5[W/m^2]
\]
いま室内の熱量は1辺5mの壁面と天井を通して外に伝わります。床面は断熱されているため除外します。つまり伝熱面積Aは側面4面と天井面の5面になります。それぞれの面の面積は5×5=25m²であるため、伝熱面積Aは25 m²×5面=125m²となります。

よって消費電力はq×A=50.5×125=6312.5［W］≅6.3［kW］となります。

 

（３）熱伝達係数について補足

実際に伝熱の計算を行うときに最も悩むのが熱伝達係数をいくつにするか？だと思います。熱伝導係数は材料固有の値（例えば鉄系材料では約11.8×10^-6/℃）になりますが、熱伝達係数は流れの状態や流れの中に置かれる物体の形状によって異なる値を示すためです。

このため形状が複雑になればなるほど熱流体解析はCFD（Computer Fluid Dynamics）の力を借りるか実験を行う必要があります。一方で簡単な形状であればヌセルト数の実験式から求めることができます。

 

ここでヌセルト数の定義について確認します。

流体の熱伝達率h、流体の熱伝導率λ、代表長さL、ヌセルト数Nu

Nu=hL/λ

∴h=Nu・λ/L

 

ヌセルト数がわかれば定義式から熱伝達率hを逆算することができます。

いくつかの実験式を表1に示しますのでご参考ください。

 

表1　いくつかの流れにおけるヌセルト数の実験式

流路	対流		実験式	Pr数
滑らかな平板上	強制対流	層流	\[ Nu=0.332×Pr^{\frac{1}{3}}Re^{\frac{1}{2}} \]	0.6＜Pr＜15
		乱流	\[ Nu=0.0296×Re^{\frac{4}{5}} \]	Pr=1
平板上下	自然対流	層流	\[ Nu=0.54（GrPr）^{\frac{1}{4}}：A側 \]	\[ 10^5＜GrPr＜2×10^7 \]
		乱流	\[ Nu=0.14（GrPr）^{\frac{1}{3}}　：A側 \]	\[ 2×10^7＜GrPr＜3×10^{10} \]
		乱流	\[ Nu=0.27（GrPr）^{\frac{1}{4}}　：B側 \]	\[ 3×10^5＜GrPr＜3×10^{10} \]
円管内	強制対流	乱流	\[ Nu=0.023×Pr^{\frac{1}{3}}Re^{\frac{4}{5}} \]	\[ 10^4＜GrPr＜1.2×10^5 \]

Gr：グラスホフ数

\[
Gr=\frac{L^3g\beta\Delta T}{ν^2}
\]

L              ：代表長さ

g               ：重力加速度

β             ：体膨張係数

ν             ：動粘性係数

 

Pr：プラントル数（空気や水ではほぼ１）

\[
Pr=\frac{ν}{a}
\]

ａ             ：熱拡散率

 

Re：レイノルズ数

Re＝VL/ν

V              ：流速

L              ：代表長さ（円管の場合は円管直径）

以上

 

ウェビナーを開催しています！