機械設計者の基礎知識4力学に触れよう。 第4回　密封構造の設計

本連載では、技術士の春山先生に、設計者の方へ向け材料力学・機械力学・熱力学・流体力学の「4力」について解説いただいています。実務で使用できる例題をご用意しているため、日々の業務に取り入れやすい内容です。

第四回は材料力学・流体力学を用いた密封構造の設計について、例題を解説します。

 

はじめに

機械はしばしば密封する必要があります。密封するために必要な構造は経験値で出せる部分もありますが、ある程度は計算できます。例えば密封でよく使われるOリング。硬度A70、直径φ2.4のOリングを0.7㎜潰して密封する場合、およそ3.2N/mmの力が必要です（ここまではJIS規格やメーカーカタログで確認可能）。フランジをボルトで締結する構造を新規設計する場合、ボルトサイズや本数、締め付けトルクはいくつにすればよいでしょうか。あるいは密封のために溶接を行うことがあります。密封だけなら良いのですが、内部から圧力を受ける場合の強度は大丈夫でしょうか？いずれも基礎的な材料力学の知識があれば算出できます。

本来、機械設計を行う者には基礎的な力学知識が必要なのです。

 

［１］予備知識

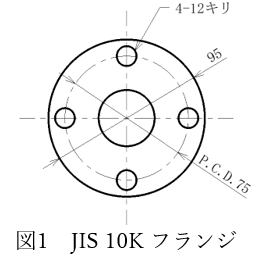配管のフランジではJIS規格のフランジがよく用いられます。例えば25AのJIS10Kフランジは外径φ95、板厚10、ボルトサイズM10×4本（P.C.D.75）となります。

また、5K、10K、16Kという呼びは必ずしも耐圧を表しているものではありません。

例えば10Kであれば温度依存があるので―20℃から120℃までですと、1.4MPaの耐圧になります。

 

 

［２］Oリングを使った密封フランジの設計

Oリングを使った密封フランジを自分で設計する場合はおおよそ次の手順を確認します。

（１）手順

①用途は？（運動用、固定用、真空用など）

②内圧か外圧か？（固定用の場合）

③Oリングのサイズ、つぶし代

 

①用途は？

運動用の場合、P（Packing）規格

固定用の場合、G（Gasket）規格

真空用の場合、V（Vacuum）規格

 

用途に合わせて規格を選びます。

 

②内圧か外圧か？

Oリングで密封する際にはOリングを保持するための形状を設計します。これはJIS B 2401-2、ハウジングの形状・寸法に詳細記載があります。

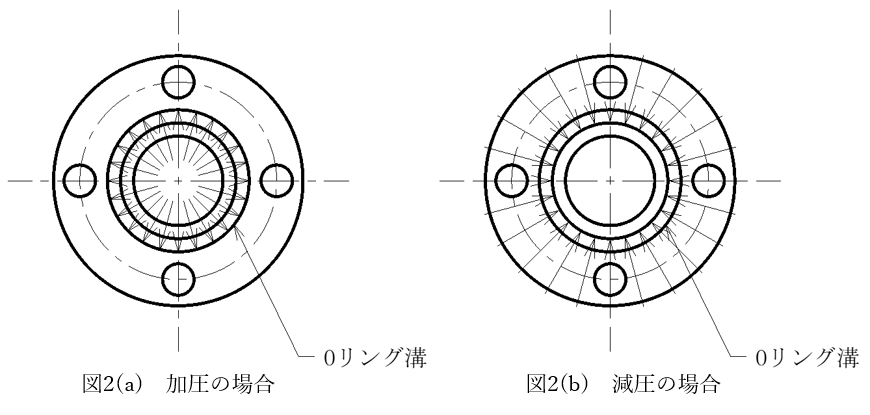
形状を設計するにあたっての注意点として、内圧か外圧か？で考え方が少し異なります。溝を設計することを考えます。図2.aに示すように内圧の場合、Oリングは外に押し広げられて外径で密封することになるため溝の設計は外形基準での設計になります。外圧の場合は図2.bの通りで内径基準での設計になります。

・内圧とは内部から外部に向かって圧力が働く状態を言います。

・外圧とは倍部から内部に向かって圧力が働く状態を言います。真空引きが該当します。

 

③Oリングのサイズ、つぶし代

密封対象の大きさと用途（P、G、V）が決まればOリングの選定ができます。このときOリングの線形も決まります。そして線形が決まればOリング溝の設計が決まり、つぶし代が分かります。

Oリングの圧縮力はOリングの硬度（材質に依存）とつぶし代がわかればメーカーサイトなどから得ることができます。

 

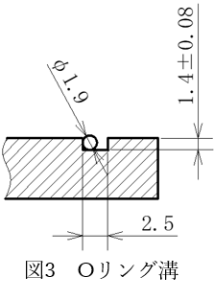例えばP3を選定し、材質はNBR硬度A70とします。このとき溝寸法は図3に示す通りh=1.4±0.05、Oリングの線径はφ1.9±0.08となり、Oリングのつぶし代は最大0.63～最小0.37となります。

硬度A70、線形1.9つぶし代0.63の場合に必要な圧縮力はおよそ3.5N/mｍになります。

 

 

 

 

 

（２）角フランジ設計例

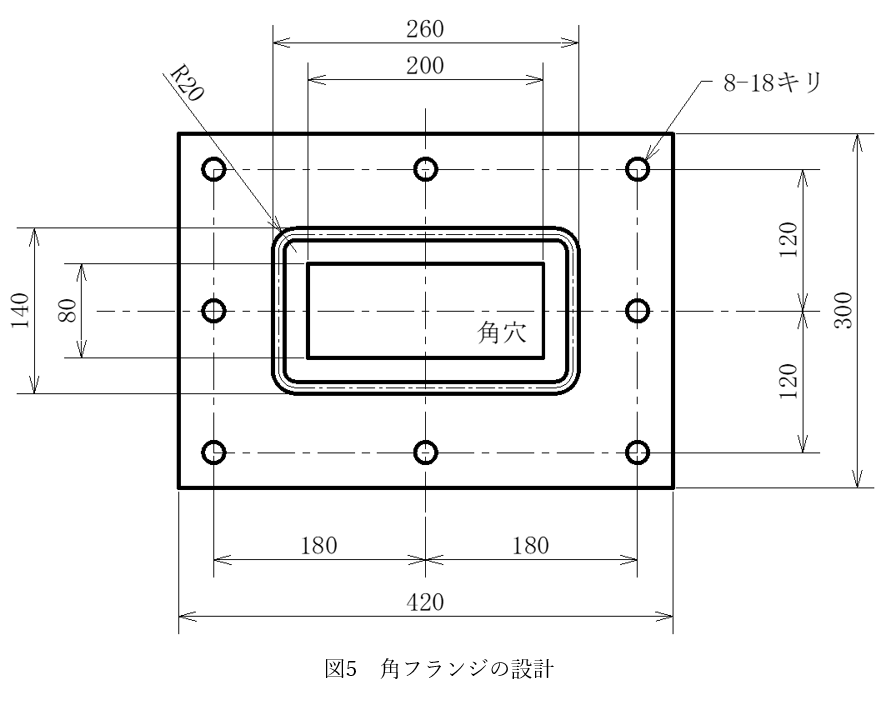
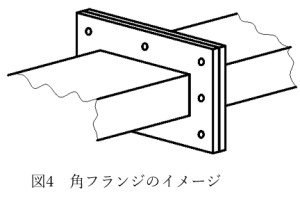図4に示すような角フランジを設計しました。用途は固定です。詳細を図5に示します。外径は420×300、流体の通る流路として角穴200×80が開いています。フランジ固定用にφ18のキリ穴を8カ所を開けています。これはM16ボルトでとめます。

このフランジにいま内圧（加圧）1.0MPaがかかるとします。このときＯリング溝を設計するにあたり、暫定的に外寸法を260×140、角部のRをR20としました。

 

 

 

先のステップに従い確認していきます。

①用途

固定用のためG規格のOリングを選定します。

 

②加圧か減圧か。

今回は加圧になります。よって外形基準の設計になります。

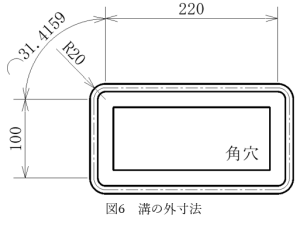
いま外寸法が260×140、R20のため溝の外周長さは図6に示すようになります。すなわち

220×2＋100×2＋31.4×4＝765.6

 

 

長さL=765．6をもつ円直径dは

d=L/π=765．6/π=243.7

 

③Oリングのサイズ、つぶし代

外径がφ243.7を超えずかつ、最も近い数字を持つG規格のOリングはG-230です。

G-230　線形（太さ）φ5.7　、　内径φ229.3　、　外径φ240.7

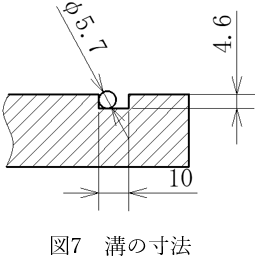
よってG-230を選定します。これにより線形がφ5.7と決まり、図7のように自ずと溝寸法も決まります。

今回の場合、溝の深さが4.6となり、Oリングの線形がφ5.7のためOリングのつぶし代は5.7-4.6=1.1㎜となります。＊ここでは簡単のため公差を無視します。

仮に使用するOリングの硬さがA70だった場合（硬さは材質に依存します）、φ5.7の線径を持つOリングを1.1㎜をつぶすために必要な力はメーカーサイトなどから得られます。ここでは2.7N/mm とします。

 

 

[補足]

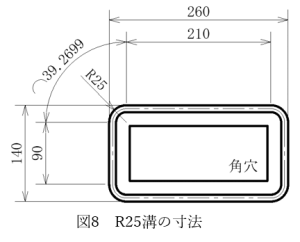図5に示すように□260×140の形状の角部をR20取った場合、その外周長さは図6に示すようにL＝765.6になります。

この長差の外周を直径換算するとφ243.7であり、外形φ240.7をもつG-230を選定しました。仮に一つ上のG-235を選定すると、外形φ245.7であり溝の外周よりもOリングの外周の長さの方が長くなってしまいます。つまり、溝の中にOリングが入り切りません。

よって、内圧がかかる場合は外側基準でOリングの長さに合わせて溝を設計します。

 

□260×140-R20の場合、外周長さは765.6

G-230　Oリング外周長さは756.2であり、Oリングの方が9㎜程短いため溝に入れることができます。

例えば角部のRをより大きくするとどうなるか見てみたいと思います。

具体的にはR25にします。

 

□260×140-R25の場合、外周長さは757.1

外周長さL=210×2+90×2+39.2699×4=757.1（図8より）

Oリング外周756.2に対し、0.9㎜だけ長い外周を持つ溝になります。R20に比べてよりOリングの外周に近い長さになりましたが、Oリングには公差があるためあまりにギリギリの寸法にしてしまうと、場合によってはOリングの方が長くなってしまうことがあるので注意が必要です。

例：G-230の寸法公差　線径（太さ）5.7±0.13、内径φ229.3±1.73

 

［補足終わり］

 

 

さてここでOリングをつぶすために、2.7N/mmの分布荷重を得ようとしたときに1本当たりのボルトの軸力はいくら必要でしょうか。

 

ここでフランジを剛体と考えます。分布荷重をｗ、ボルト間の距離をＬ、軸力をＦとすると

 

Ｆ=ｗＬ/2

 

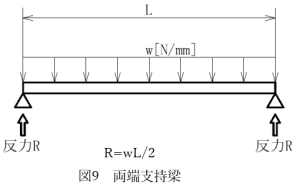となります。これは図9に示すように、等分布荷重を受ける両端固定梁の支点反力の式から得られます。

 

よって今回の場合、Ｏリングをつぶすために必要なボルトの軸力は

2.7×180/2=243［Ｎ］・・・(a)

 

となります。

 

まとめると、

・ボルトの最大ピッチが180。

・G-230硬度A70のOリングをつぶすためには等分布荷重2.7N/mm以上が必要。

・フランジ部を剛体と考える。（考えてよいだけの厚みを持つ。）

・等分布荷重ｗを受ける両端固定梁の両端に発生する反力RはR＝wl/2

・軸力はこの反力以上の力が出ないとＯリングをつぶすことができない。

 

ではさらに、M16ボルトの軸力はいくつになるでしょうか。

 

 

（３）ボルトの軸力

ボルトの軸力Fはボルトの呼び径d、締め付けトルクT、トルク係数kから次式で与えられます。

F=T/kd

 

いま締付トルクにはT系列と呼ばれるものを採用しM16ボルトのトルクを確認すると、106N/mになります。

被締結材をsus-susとすると、トルク係数はおよそ0.45になります。

よってM16の場合の軸力は次の通りです。

 

Ｆ=106×10³／0.45／16=14,722［Ｎ］

 

M８からM16 までをT系列の締付トルク、トルク係数0.45としたときの軸力計算結果を表1に示します。

 

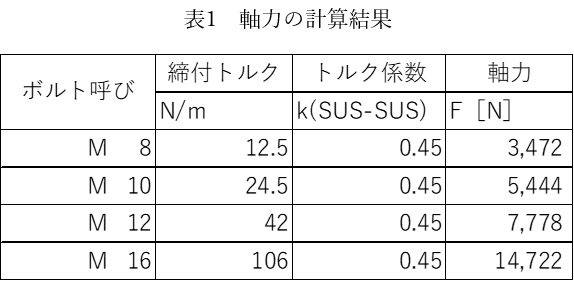
先に見たように要求される最低の軸力は243［N］に対し、M16は適正トルクで締め付けることで14,722［N］の力が出ます。

パッキンをつぶすために十分な軸力であり楽に締め付けられると思います。もしこれがM3ボルトだった場合、その軸力は467Nになります。当然、ボルト径が小さい方が軸力が小さくなりますが、よほどの制約があって小さなボルトを選定する必要がある場合でなければ特に問題はないかと思います。

もし小さなボルトを選定する必要がある場合は、

・ボルトピッチをなるべく小さくする。

・ボルトの強度区分を10.9や12.9（いわゆるハイテンボルト）に変更して締め付けトルクを大きくする。

などの対応が考えられます。

私の経験上ではボルト固定するフランジの場合、設計要因での不具合よりもその他の要因での不具合が多かったです。

ウェビナーの方でいくつかの失敗事例を紹介させていただきます。

 

［３］溶接継手の強度

（1）　すみ肉溶接部の強度についての解説

フランジとフランジを密封させるためのOリングの選定やハウジング形状はJIS規格やメーカーサイト・カタログ値から決めることができます。

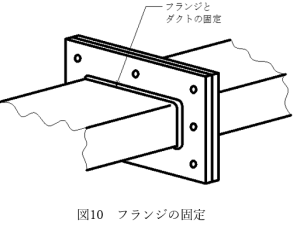
ここからは、図10に示すようにフランジそのものをダクト、配管に固定する方法、溶接について見ていきます。

 

通常、密封のために溶接を行う場合は図11に示すように全周溶接指示（図11は全周すみ肉溶接）を行います。

 

 

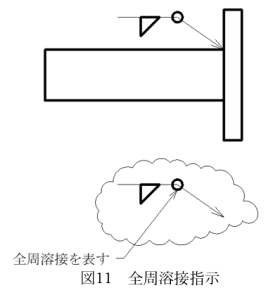
ここで内圧がかかる場合は、溶接部の強度にも注意が必要です。内圧がかかる場合、図12のように任意断面にはその断面を内圧により引き裂こうとする力Fが発生するためです。

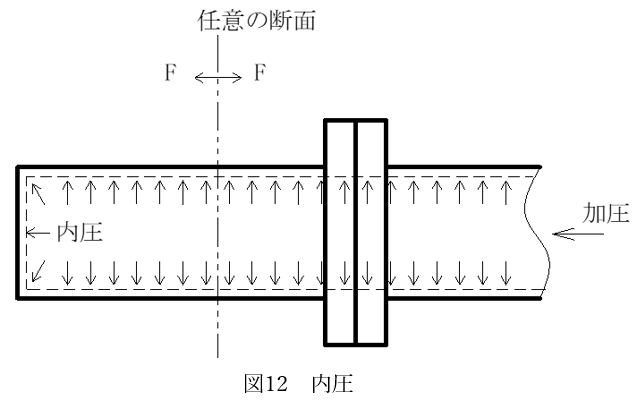
この力Fは内圧Pと内部の断面積Aの積で得られます。すなわち

 

F［N］=P［N/m㎡］×A［m㎡］

 

では任意断面を溶接部にとり、この力Fが溶接部に作用するときを考えて溶接部の強度を確認します。

溶接部と言えども応力σの定義は、作用する力Ｆとそれを受ける断面積の比です。

σ=Ｆ／Ａ

 

溶接の場合、力Fを受ける断面積は［のど厚a×溶接長さL］になります。

等脚すみ肉溶接の場合、図13に示す部分がのど厚であり、その長さは

（のど厚a）=（脚長S）／√2になります。

 

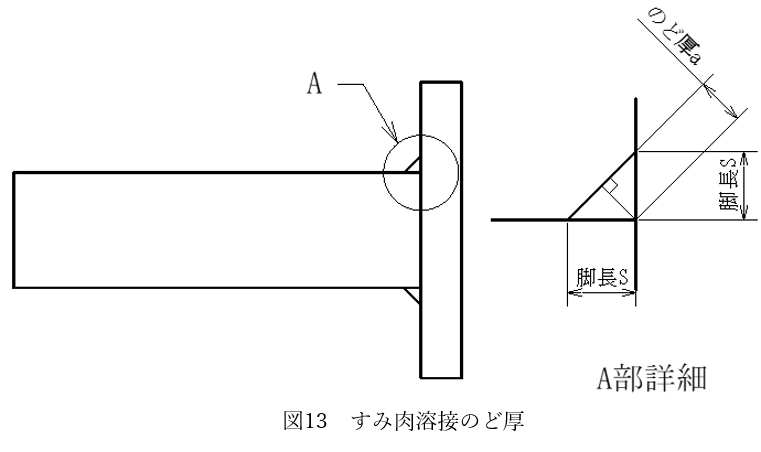
よって発生する応力は

σ=F／［S/√2×L］

ただし、この力を受ける面積（のど厚）は力の作用する方向に対し垂直ではありません。45°傾きを持っています。この場合、引っ張り応力はゼロ、せん断応力が最大となります。

このような溶接の強度評価は、鋼構造設計基準、道路橋示方書から、材料の降伏強さをσyとすると、

σy／1.5√3

 

例えばSM490で厚みが16㎜以下の場合、降伏強さは325N/m㎡以上になります。

よって許容応力は

325／1.5√3＝125.1N/m㎡

となります。

 

（2）　すみ肉溶接部の強度についての計算例

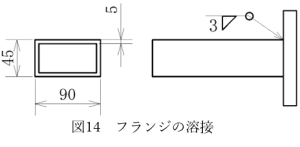いま、図14に示すように45×90、板厚t5の角ダクトにフランジを溶接します。

溶接はすみ肉溶接で脚長は3mmです。

他条件は以下の通りです。

 

・内圧１.0MPa

・材料降伏点235N/m㎡

 

このとき溶接部の強度を確認していきます。

 

①溶接部にかかる力Fの計算

F=内圧×断面積

F=1.0×｛（90-2t）×（45-2t）｝＝1.0×｛（90-2×5）×（45-2×5）｝

＝1.0×80×35=2800［N］

 

②溶接部面積の計算

・溶接長さLは角ダクトの外周を全周溶接です。よってL=90+45+90+45=270mm

・のど厚a＝3／√2=2.12mm

よって断面積A＝L×a＝270×2.12=572.4［m㎡］

 

③発生する応力σ

σ=F／A=2800／572.4=4.9［N／m㎡］

 

④許容応力σa

σa=σy／1.5√3=235／1.5√3＝90.4［N／m㎡］

 

σa>σ（90.4>4.9）であるため強度上問題はない。

 

 

（３）その他の溶接指示におけるのど厚a

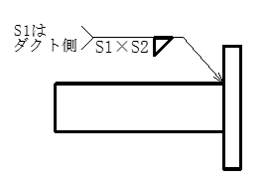
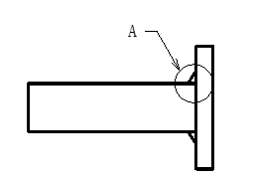
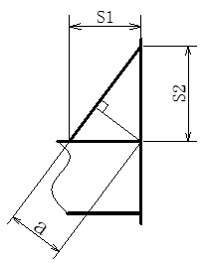
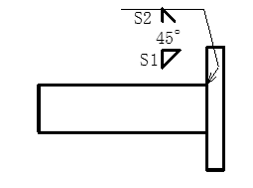
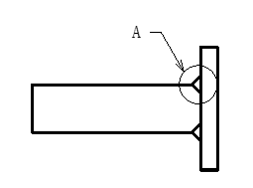
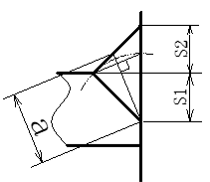
不等脚すみ肉溶接および、すみ肉とレ型開先を組合わせた場合ののど厚の図を表2に示します。

 

①不等脚すみ肉溶接

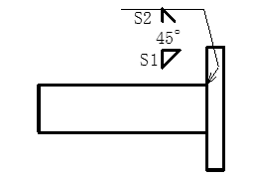
S1＜S2の場合、\( a=\frac{s1×s2}{\sqrt{s1^2 + s2^2}}\)となります。

②すみ肉とレ型開先の組合せ

S1=S2=Sのとき、a=S√2／sin67.5　となります。

（詳細はウェビナーで解説いたします。）

 

溶接指示	溶接姿	のど厚a

 

チャレンジ問題

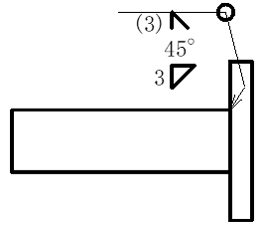
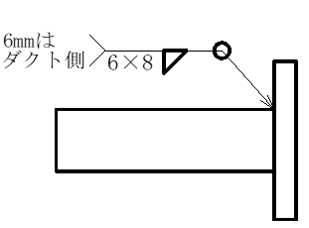
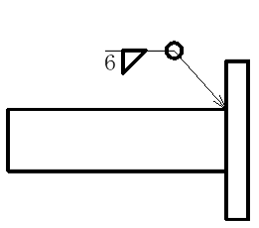
（１）角ダクトに角フランジを溶接する。次の溶接指示の中で最も強度が強くなるものはどれか。正しいものを選べ。溶接長さは全て同じとする。

解答選択欄①	解答選択欄②	解答選択欄③

 

（2）不等脚すみ肉溶接のとき\( a=\frac{s1×s2}{\sqrt{s1^2 + s2^2}}\)となることを示せ。

 

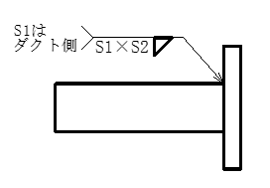
（3）すみ肉とレ型開先の組合せにおいて、S1=S2=Sのとき、a=S√2／sin67.5　となることを示せ。

 

ウェビナーを開催しています！