機械設計者の基礎知識4力学に触れよう。 第6回　ピック＆プレイスにかかる時間

本連載では、技術士の春山先生に、設計者の方へ向け材料力学・機械力学・熱力学・流体力学の「4力」について解説いただいています。実務で使用できる例題をご用意しているため、日々の業務に取り入れやすい内容です。

第六回　ピック＆プレイスにかかる時間は機械力学を用いた計算方法について、例題を用い解説します。

 

はじめに

自動機械の動作でピック＆プレイスを行うことがあります。文字通りある場所に置かれた部品をピック（掴む）して別の場所にプレイス（置く）することです。部品を整列させたり組立を行なったりする動作がそれです。ところで自動機械を設計する場合、サイクルタイムを評価する必要が頻繁にあります。A点からB点へのピック＆プレイスには何秒かかるでしょうか。この計算には機械力学の基礎知識が必要になります。

本来、機械設計を行う者には基礎的な力学知識が必要なのです。

 

１．直線運動と回転運動

・直線運動

質量mのある物体が初速ゼロから加速度a［m/s²］で直線運動を始め、t秒後に最高速度v［m/s］に到達したとします。その後T秒間、速度vで移動して加速度-aで減速をしてt秒後に速度がゼロになりました。このときの移動距離をx［m］とします。

この質量mの速度を縦軸に、経過時間を横軸に取ったものが図1.1になります。t秒間加速して速度vに到達。そのT秒後に加速度-aで減速して減速開始からt秒後に速度がゼロになります。

また、質量mの移動距離を縦軸に、経過時間を横軸に取ったものが図1.2になります。

 

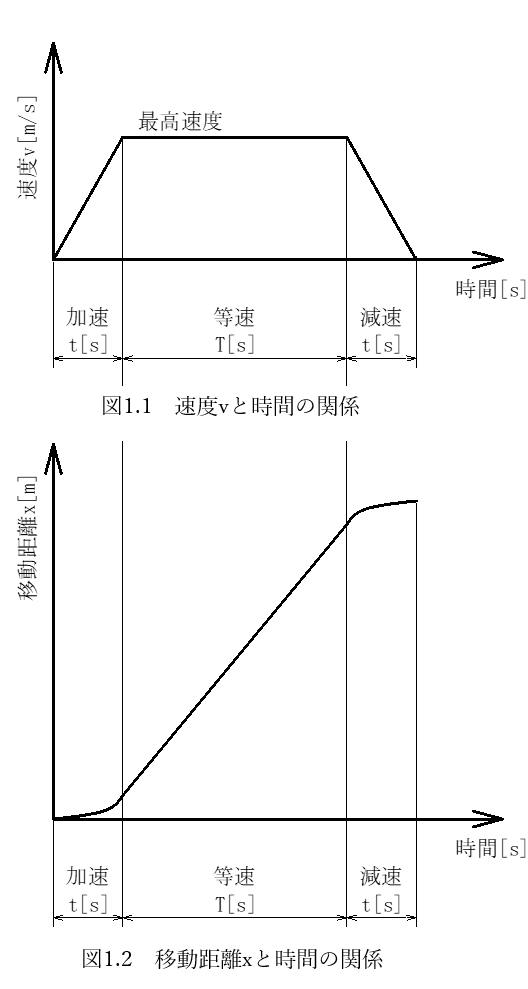
移動距離ｘ、速度ｖ、加速度aとしたときにそれぞれの関係性は次の通りです。
\[
v=\frac{dx}{dt}
\]
\[
a=\frac{d^2x}{dt^2}
\]
初速がゼロの場合、加速初めからt秒後の移動距離x1
\[
x_1=\frac{1}{2}at^2
\]
速度vでT秒間移動した際の移動距離x2
\[
x_2=vT
\]
速度vから加速度-aで減速しt秒後にゼロになったときの移動距離x3
\[
x_3=\frac{1}{2}at^2
\]
よってこのときの総移動距離ｘは
\[
x=x_1+x_2+x_3=\frac{1}{2}at^2+vT+\frac{1}{2}at^2
\]
\[
x=at^2+VT
\]
となります。

 

以上の関係性を図2に整理します。

 

ここでは速度と加速度、時間から移動距離を計算していますが、Ａ点からＢ点へ移動という形で移動距離と加速度、最高速度を与えると移動にかかる時間を計算することができます。

 

 

・回転運動

中心からrの位置にある質量mが初速ゼロから角加速度α［rad/s²］で回転運動を始め、t秒後に最高角速度ω［rad/s］に到達したとします。その後T秒間、角速度ωで回転を続け、角加速度-αで減速をしてt秒後に角速度がゼロになりました。このときの回転量をθ［rad］とします。

この質量mの角速度を縦軸に、経過時間を横軸に取ったものが図3.1になります。t秒間加速して角速度ωに到達。そのT秒後に加速度-αで減速して減速開始からt秒後に角速度がゼロになります。

また、質量mの回転量を縦軸に、経過時間を横軸に取ったものが図3.2になります。

 

回転量θ、角速度ω、角加速度αとしたときにそれぞれの関係性は次の通りです。

＊図を見ていただくと分かる通り、直線運動と同じ関係性を持ちます。

\[
\omega =\frac{d\theta}{dt}
\]
\[
\alpha =\frac{d^2\theta}{dt^2}
\]
初速がゼロの場合、加速初めからt秒後の回転量θ₁
\[
\theta_1 =\frac{1}{2}\alpha t
\]
角速度ωでT秒間回転した際の回転量θ₂
\[
\theta_2 =\omega T
\]
角速度ωから角加速度-αで減速しt秒後にゼロになったときの回転量θ₃
\[
\theta_3 =\frac{1}{2}\alpha t^2
\]
よってこのときの総回転量 は
\[
\theta=\theta_1+\theta_2+\theta_3=\frac{1}{2}\alpha t^2+\omega T +\frac{1}{2}\alpha t^2
\]
\[
\theta=\alpha t^2+ \omega T
\]
となります。

 

こちらの関係性を整理したものが図4になります。直線と比べると関係性は同じであることが分かります。

 

 

［２］運動の方向（速度ベクトル）

参考に一つ問題を出します。

問題　回転と直線運動の組合せ

図5のように回転運動するアームAの先端に直線運動するアームBが付けられています。アームAが反時計回りに角速度ωで回転しています。このアームAが鉛直下向きに到達した時点でアームBが速度vで伸びる方向に運動しています。それぞれのアームが運動を維持したまま、アームが水平位置に到達したときのアーム先端O点における運動の方向、速度ベクトルを考えます。

 

解答

速度vのｘ方向成分をv_x、y方向成分をv_yとします。

また、回転による速度成分には添え字1をつけてv₁（v_x1、v_y1）、直線運動によるものには添え字2を付けてv₂（v_x2、v_y2）とします。また、アームが水平方向となす角をθとします。つまりアームが水平方向にいるとθ=0です。

 

このとき、回転運動による速度成分は次の通りです。回転運動における回転角度と速度成分の関係性は図6.1に示す通りです。

\[
v_{x1}=v_1 \sin\theta=0
\]
\[
v_{y1}=v_1 \cos\theta=v_1
\]

直線運動による速度成分は次の通りです。直線運動における回転角度と速度成分の関係性は図6.2に示す通りです。
\[
v_{x2}=v \cos\theta=v
\]
\[
v_{y2}=v \sin\theta=0
\]
よってアーム先端O点のx方向y方向それぞれの速度成分v_x、v_yは次の通りになります。
\[
v_x=v_{x1} +v_{x2}=0+v
\]
\[
v_y=v_{y1} +v_{y2}=v_1+0=\gamma\omega
\]
\[
v_y=v_{y1} +v_{y2}=v_1+0=\gamma\omega
\]
\[
\overline{v}=
\{
\begin{array}{rr}
v& \\
\gamma&\omega \\
\end{array}
\}
\]
\[
v=\sqrt{v^2+(\gamma\omega)^2}
\]

［３］ピック＆プレイスにかかる時間

次のような問題を考えます。

 

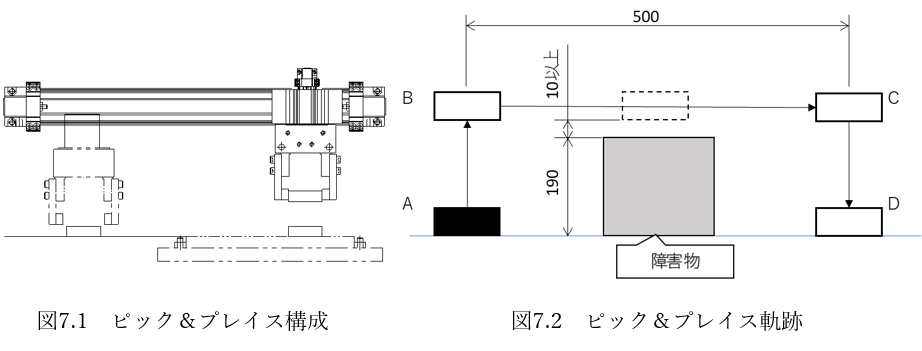
図7.1、7.2に示すように、A点でワークをピックし、障害物を避けるためにB点→C点と通り、D点にプレイスします。A点からB点までの移動距離は200㎜、B点からC点は500㎜、C点からD点は200㎜となります。

上下移動、水平移動ともに最大速度を200㎜/s、加速時間を0.5秒とします。

＊通常、エアシリンダでは加速度や速度を事前に検討することはかなり難しいですが、ロボシリンダなどを使えば加速度や最高速度を設定値として定めることができます。

解答

 

 

図8.1、図8.2にそれぞれ移動距離と時間、速度と時間の関係を示します。

まずは加速度を求めます。
\[
a=\frac{v}{t}=\frac{200}{0.5}=400[mm/s^2]
\]
＊加速時間ではなく加速度が与えられる場合は、加速度と最高速度から加速時間を計算します。

加速中の移動距離をx1とします。
\[
x_1=\frac{1}{2}at=\frac{1}{2}×400×0.5^2=50[mm]
\]
A→Bの移動距離は200㎜のため、加減速で50㎜×2=100㎜移動します。つまり等速では200-100=100㎜移動することになります。速度200mm/sで100㎜移動したときの経過時間は100/200=0.5[s]となります。

よってA→Bの移動にかかる時間Tabは

Tab=0.5+0.5+0.5=1.5[s]になります。

 

同様に

B→C区間は3.0（0.5s+2.0s+0.5s）

C→D区間は1.5（0.5s+0.5s+0.5s）

となります。

 

A→Dへの移動には6.0秒かかります。

Tad=1.5s+3.0s+1.5s=6.0s

 

以上の通り、移動距離と最高速度および加速時間（あるいは加速度）がわかれば移動にかかる時間を算出することができます。

 

 

［４］チャレンジ問題

ピック＆プレイス動作をするさいに、サイクルタイム短縮目的でアーチモーションを取り入れることがあります。

アーチモーションについて補足します。先の問題で見たピック＆プレイスの動作は障害物をかわすためにA→B→C→Ｄと動きます。

まずA→B→Cの動きに着目します。アーチモーションでは上下運動をＢ点で止めずにＢ‘まで移動させます。このとき移動がB点に到達した時点で水平移動（B→C）の移動を開始させます。

次にB→C→Dの動きに着目すると水平移動（B→C移動）がC点に到達する前、C’点で下降を開始します。

整理したものを図9に示します。

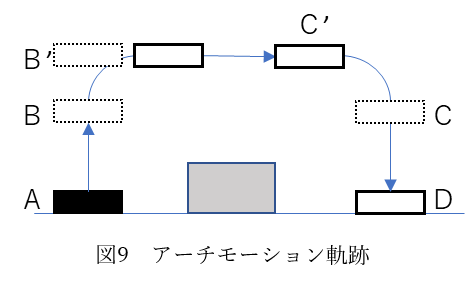
このとき、機械の動く距離はアーチモーション前と比べて長くなります。しかしA点からD点への軌跡を適切にとることで、A→Dへの移動のサイクルタイムは短縮されます。

 

さてここで問題です。アーチモーションを取り入れる前のサイクルタイムは6.0秒でした。アーチモーション取り入れた際、最短でサイクルタイムは何秒になるでしょうか。

 

解答はぜひウェビナーをご覧ください。

 

ウェビナーを開催しています！