1ランク上の品質、コストを実現する幾何公差の逆転活用法 第4回 規則編「よくある間違いには気をつける」
技術士の折川先生による連載「1ランク上の品質、コストを実現する幾何公差の逆転活用法」です。第4回は規則編「よくある間違いには気をつける」です。
目次
はじめに
前回までに、機能品質やコストを適正化するための幾何公差の基本的な考え方について解説した。
この幾何公差を効果的に活用するためには、その文法や作法を正しく理解しておく必要がある。
最終回の今回は、幾何公差の運用ルールに焦点を当て、理解しているようでも実は間違った使い方をしている事例を紹介しながら、使用上の注意点について解説する。
1. 幾何公差は共通言語
1-1. モノづくりのグローバル化と協業化

図 1 モノづくりのグローバル化と協業化
図1は現在のモノづくりの実態を簡略的に表現したものである。
国際経済や社会情勢の影響についてここでは細かくは述べないが、同図左に示すように、モノづくりは海外との関わりが非常に強くなっている。
そのため、相手先との設計情報の授受は頻繫に行われる。
一方、国内においても同右図に示すように、複数の会社間との協業により、設計情報の共有も同様に頻繫に行われている。
いずれの場合も、モノづくりのための設計情報は、相手先に確実にその意図が伝わり、正しく共有できている必要がある。
1-2. 設計情報、設計意図の確実な伝達
設計情報である図面の公差指示は、部品形状のばらつきを、設計意図に沿って規制する手段であり、これはすなわち設計上のノウハウでもある。
国内外を問わず、共通言語としての幾何公差を活用して、部品の幾何学的特性(形状/姿勢/位置)および、取り付けや組み立てに関する設計意図を表現するためには、幾何公差の基本的作法、文法を理解し、相手に、正確にわかりやすく、設計意図を伝達しなければならない。
当然、間違った用法は、想定外のトラブルに繋がる。
次節から、この幾何公差の、注意すべき用法について説明する。
2. よくある間違い― 文法編
2-1. 平面度

図 2 平面度の注意点
平面度は平面の形状偏差を規制する。
形状偏差はその形体自体の理想的な形状からのずれであり、何かを基準として評価するものではない。
したがって、データムを参照することはない(図2)。
なお本図以降、参考のため、☆印を使って要注意度レベルを示してある。
★の数が多いほど、間違えやすく要注意であることを意味する。
2-2. 真円度、円筒度
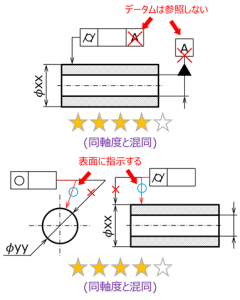
図 3 真円度、円筒度の注意点
真円度、円筒度は円筒面の形状偏差を規制する。
これも前記の平面度と同様の理由から、データムを参照することはない(図3上)。
また、規制しているのは表面形体であるため、同図下のように、直径寸法線に揃えないで配置する。
これらの間違いは、真円度や円筒度を同軸度、同心度と混同している場合に多い。
2-3. 平行度

図 4 平行度の注意点
平行度は基準に対する姿勢偏差を規制する。
姿勢は、何かを基準にして平行か否かを判断するため、平行度は必ずその基準としてのデータムを参照する(図4上)。
この間違いは滅多にないが、同じ姿勢偏差の直角度にも当てはまるので注意する。
平行度でたまに見かける間違いに、位置度と混同しているケースがある。
図4下のように、平行度を指示した面への寸法はサイズ公差による寸法であり、TED(理論的に正確な寸法)にはしない。
2-4. 傾斜度

図 5 傾斜度の注意点
傾斜度は基準からの姿勢偏差を規制する。
同じ姿勢偏差の仲間である平行度は、平行2平面間のサイズ公差による寸法指示だが、傾斜度の場合は、角度寸法を必ずTEDにする(図5上)。
ちなみに、平行2平面の間には角度0°のTEDが暗黙の寸法として入っており、一般にそれは図示されないため、表には表示されていない、と解釈する。
傾斜度で比較的多い間違いは、公差値に角度記号を入れるケースである。
幾何公差は平行2平面・曲面の間または円筒・球の公差域のみを持ち、角度による指示はしない。
図5下に示すように、傾斜度の公差域は、斜面をはさんだ平行2平面の間であることに注意する。
2-5. 同軸度、同心度

図 6 同軸度、同心度の注意点
同軸度、同心度は中心線の位置偏差を規制する。
表面への指示ではないため、幾何公差の指示線は必ず寸法線に揃える(図6)。
同図のような間違いは、同軸度や同心度を真円度、円筒度と混同している場合に多い。
逆に2-2項で述べたように、真円度や円筒度の指示先を寸法線に揃える、という間違いもあるため、同軸度/同心度と真円度/円筒度の区別には十分注意が必要である。
2-6. 円筒公差域
円筒公差域は幾何公差に特有の公差域指定方法である。
この公差域で規制するのは、中心線の位置だけであり、表面に対して用いることはない。
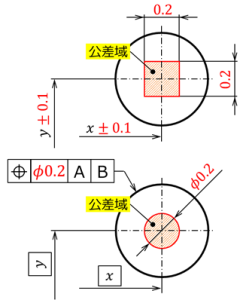
図 7 円筒公差域

図7上はサイズ公差で指示した場合の公差域で、この例では、x方向とy方向にそれぞれ幅で0.2の正方形の公差域が設定されている。
同図下は幾何公差で指示した場合の公差域で、位置度の公差値としてΦ0.2を指定している。
この場合の公差域は、TEDで指定されたxとyの理想的な位置を中心とした、直径Φ0.2の公差域となる。
サイズ公差の公差域では、対角方向に公差の緩い領域が生じるが、この円筒公差域にはそれがなく、中心線の位置をより厳密に規制できる。
円筒公差域を適用できる幾何公差には種類があり、同図右に、それを適用できるものとできないものを表形式で掲載した。
次に、この円筒公差域の適用で間違えやすい事例を紹介する。
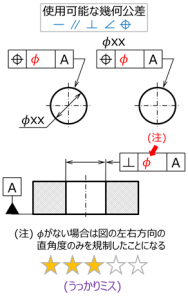
図 8 円筒公差域の注意点1
まず最初は、円筒公差域を使用可能な幾何公差のグループでの間違いの例である(図8)。
多くは、単にΦを入れ忘れることだが、意外とこの間違いは多い。
ここで、同図下の例は注意が必要である。
この直角度の指示において、Φのない場合は、図の左右方向の直角度(中心線の傾き)のみを規制したことになる。
幾何公差の文法的には間違いはないため、紙面に垂直な方向の中心線の傾きが意図とは異なる可能性がある。
同様なケースは、同じ姿勢偏差を規制する平行度や傾斜度でもあり、この例のように、円筒公差域を指定するか否かは、設計仕様に合わせ、適切に使い分ける必要がある。
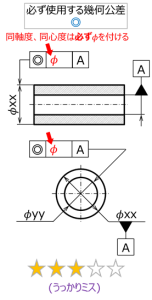
図 9 円筒公差域の注意点2
次は、円筒公差域を必ず使用する幾何公差グループでの間違いの例だが、これには同軸度、同心度の2つのみが該当する(図9)。
同軸度と同心度は中心線の位置を規制するが、他の幾何公差と異なり、公差域は必ず円筒公差域である。このときにΦを付け忘れる間違いが比較的多い。
Φが必須であるため、万が一記入モレがあっても、それによって別の解釈をされる危険性はほぼないと思われるが、作法としてΦの抜けはないように気をつけたい。
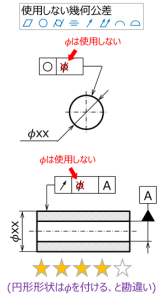
図 10 円筒公差域の注意点3
最後は、円筒公差域を使用しない幾何公差のグループでの間違いの例である。
非常に多い間違いは、真円度、円筒度や振れの公差にΦを付けてしまう例である(図10)。
これらの幾何公差は基本的に円形形状に対して用いられるため、Φが必要と勘違いされるケースが多い。
Φが付くことはないため、前述の同軸度、同心度と同様、別の解釈をされる危険性は少ないと思われるが、作法として気をつけたい。
2-7. データム

図 11 データム使用上の注意点
データムは、単に部品の原点基準だけでなく、形体の表面や中心線/面の姿勢や位置を規制するための基準でもある。
設計時には多くの場合、最初に基準としてのデータムを配置するが、その際に比較的間違いやすい要素の一つでもある。
図11上は、中心線に対して直接データムを指定した例であるが、この図例のように中心線を共有する複数の円筒形体がある場合に、どちらの中心線を基準とするのかがあいまいである。
古い規格ではこれでも可であったが、現在は中心線指示の場合は、寸法線に揃えて記入する。
また同図下のような間違い例も多い。
データムは必ず幾何公差によって参照される。言い換えれば幾何公差に参照されないデータムは、図面上に配置してはいけない。
部品のx,y,zの基準を設定することは普通に行われるが、図例のように、穴の中心線のデータムAに対する直角度だけが重要な場合は、データムBやCに該当する基準は基準線だけ描けば十分である。
2-8. 幾何公差

図 12 幾何公差指示上の注意点
幾何公差の歴史は意外と古く、そのため初期には許容されたが現在では不可である表記方法が散見される。
図12はいずれも古い指示方法の例である。
同図上は、中心線に直接指示した例であるが、データムの項で述べたように現在はこのような指示方法ではなく、寸法線に揃えて記入する。
同図中央は、幾何公差とデータムを一体化した表記方法であるが、現在はデータムは記号を用いて明示する。
同図下は、データム記入枠内に複数のデータム文字を入れた例で、現在は、データムの並び順により優先順位が決まるというルールを明確にするため、文字は個別の枠に記入する。
但し、共通データムの場合は一つの枠内に記入するが、その場合は文字をハイフンで結ぶ。
3. よくある間違い― 用法編
3-1. データム記号の指示位置
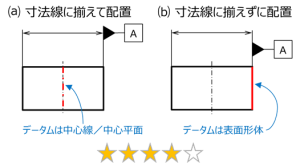
図 13 データム記号の指示位置と解釈
ここからは、文法上の間違いではないが、指示方法によって意味が異なるケースを紹介する。
図13はデータム記号の指示位置とその解釈を示したものである。
同図⒜のように、寸法線に揃えて配置した場合のデータムは中心線や中心平面である。
同図⒝のように寸法線に揃えていない場合は、データムは表面形体(この図例では右側面)となる。
データム記号の配置の位置が少し異なるだけで、形体のどの部分をデータムとして指示しているかの意味が異なるため、注意が必要である。
3-2. 幾何公差の指示位置

図 14 幾何公差の指示位置と解釈
図14は幾何公差の指示位置とその解釈を示したものである。
これは前項のデータムの場合と同様で、幾何公差記入枠からの指示線の先が寸法線に揃っているか否かで、どの形体を規制しているかの意味が異なる。
傾向的には、同図⒝の意味合いで⒜のように指示している図面を多く見かけるので、注意が必要である。
3-3. 組み合せ幾何公差

図 15 組み合せ幾何公差の公差値
ある形体の幾何特性を指示するときに、例えば平面度は厳しく規制したいが、平行度はある程度緩くてよい、という場合がある。
平行度は平面度を含んだ概念であるため、平行度を緩めると平面度も自動的に緩くなる。つまり、平行度だけで厳しい平面度も要求すると、設計仕様としては過度な平行度を設定することになる。
このような場合に使用されるのが、組み合せ幾何公差である。
図15の右に示した、位置、姿勢、形状の各幾何特性を規制する記号を複数組み合わせ、それぞれの幾何特性に合わせた公差値を指定する。
同図左は、ブロックの上面に平行度と平面度を組み合せて指示した例である。
この場合、対象面の平行度公差0.2に対して、平面度はそれより厳しく規制することが目的であり、この図のようにどちらも同じ公差値が入っていると、組み合せ幾何公差とする意味がなくなる。
この例では、平行度公差0.2より小さな、例えば0.1などの値が設定されるべきである。
組み合せ幾何公差を使う場合は、図15右の公差値の大小順に注意して、適切な公差値を与える必要がある。
4. よくある間違い― 番外編
ここまでは、2022年時点でのJIS規格(例えばJIS B0021など)に沿った、幾何公差の文法上の間違い事例について解説した。
幾何公差に関するJIS規格は基本的にISOに準拠しているが、ISOの規格はJISより数年以上先行して改定が行われている関係で、ISOの最新の規格がJISに盛り込まれていないケースがある。
例えば、図16の左上は平面度を寸法線に揃えて配置した例で、これは現行JISでは規定されていないが、中心平面に対する平面度を指示している(ASME Y14.5Mの図例を参考)。
同図左下は平面度と同じく形状偏差を規制する真直度を、中心線に対して指示した例であるが、中心平面に対する平面度指示は、この真直度指示例の平面版と考えられる。
また、図16右上は、CZ(共通公差域)を高さの異なる2面に対して指示した例で、これも現行JISには規定がないが、最新ISO(1101:2017)ではCZを従来のCommon ZoneからCombined Zoneと呼び方を変え、この図例のように同一平面上にない複数の面に対しても指示できるようになっている。
この解釈は同図右下にあるように、2つの平行度指示面の傾斜方向が同一になるような平行度の規制である。
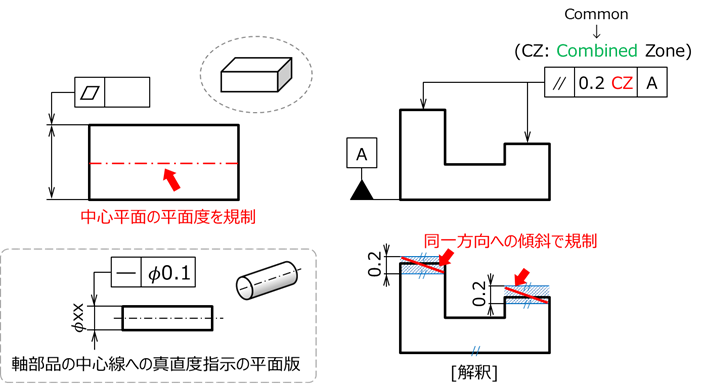
図 16 今後許容される指示方法
これらの例のように、現時点ではJIS規格外であっても、国際的には許容される表記が存在するため、特に海外との図面のやり取りがある場合は留意しておく必要がある。
まとめ
最後に、幾何公差の活用による、設計意図の正しい伝達のために理解しておくべきことを挙げる。
■基本作法の理解
幾何公差の文法・用法を、出し側/受け側の双方が正しく理解することが重要である。
相手が解釈に悩むような表現、表記は極力避けるべきであろう。
■幾何公差とサイズ公差の適切な使い分けの理解
図面指示上のあいまいさの排除が、必ずしも厳格な形体定義と同義であるとは限らない。
重要管理部位には、積極的に幾何公差を適用しつつ、ほどよい「あいまいさ」により、機能とコストを両立させることが重要である。
|
折川技術士事務所 代表 〔略歴〕 |
 |


