断面の計算
断面とは、物体を仮想切断した時にできる面です。
断面の例
断面積:断面の面積です。
断面係数:部材の曲げモーメントに対する強さを表す数値です。
断面2次モーメント:部材の曲げモーメントに対する変形し難さを表す数値です。
計算方法表
| 断面 | 重心位置 | 断面積 | 断面係数 | 断面2次モーメント |
| e【mm】 | A【mm2】 | Z【mm3】 | i【mm4】 | |
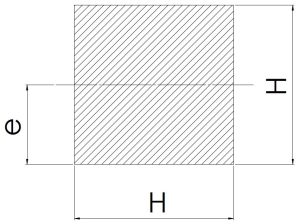 |
\[\frac {H}{2}\] | \[H^2\] | \[\frac {H^3}{6}\] | \[\frac {H^4}{12}\] |
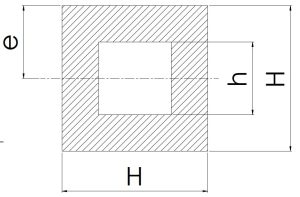 |
\[\frac {H}{2}\] | \[H^2-h^2\] | \[\frac {1}{6} × \frac {H^4-h^4}{H}\] | \[\frac {H^4-h^4}{12}\] |
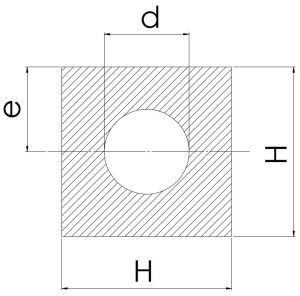 |
\[\frac {H}{2}\] | \[H^2-(\frac {πd^2}{4})\] | \[\scriptsize \frac {1}{6H}×(H^4-\frac {3π}{16}d^4)\] | \[\scriptsize \frac {1}{12}×(H^4-\frac {3π}{16}d^4)\] |
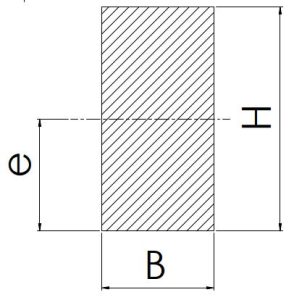 |
\[\frac {H}{2}\] | \[BH\] | \[\frac {BH^2}{6}\] | \[\frac {BH^3}{12}\] |
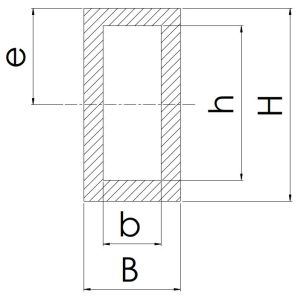 |
\[\frac {H}{2}\] | \[HB-hb\] | \[\scriptsize \frac {1}{6H}×(BH^3-bh^3)\] | \[\scriptsize \frac {1}{12}×(BH^3-bh^3)\] |
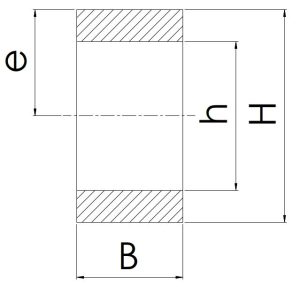 |
\[\frac {H}{2}\] | \[B(H-h)\] | \[\scriptsize \frac {B}{6H}×(H^3-h^3)\] | \[\scriptsize \frac {B}{12}×(H^3-h^3)\] |
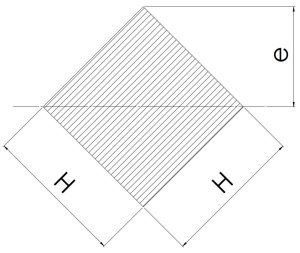 |
\[\frac{H\sqrt{2}}{2}\] | \[H^2\] | \[0.1179H^3\]\[(\frac{\sqrt{12}}{2}×H^3)\] | \[\frac {H^4}{12}\] |
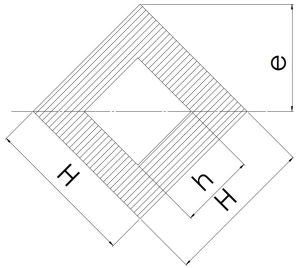 |
\[\frac {H}{2}×\sqrt{2}\] | \[H^2-h^2\] | \[\scriptsize 0.1179×(\frac{H^4-h^4}{H})\]\[\scriptsize (\frac{H^4-h^4}{12H}×\sqrt{2})\] | \[\scriptsize \frac {H^4-h^4}{12}\] |
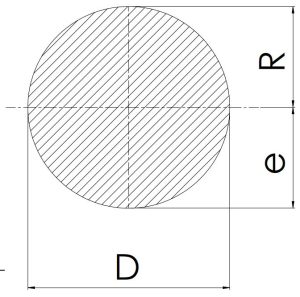 |
\[\frac {D}{2}\] | \[\frac {πD^2}{4}\]\[πR^2\] | \[\frac {πD^3}{32}\]\[(\frac {πR^3}{4})\] | \[\frac {πD^3}{64}\]\[(\frac {πR^4}{4})\] |
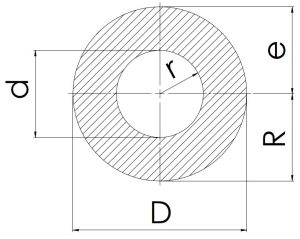 |
\[\frac {D}{2}\] | \[\frac {π}{4}×(D^2-d^2)\] | \[\scriptsize \frac {π}{32}×(\frac {D^4-d^4}{D})\]\[\scriptsize {\frac {π}{4}×(\frac {R^4-r^4}{R})}\] | \[\scriptsize \frac {π}{64}×(D^4-d^4)\]\[\scriptsize {\frac {π}{4}×(R^4-r^4)}\] |
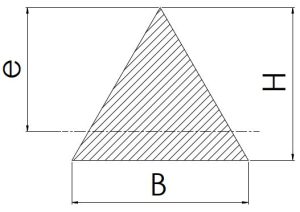 |
\[\frac {2H}{3}\] | \[\frac {BH}{2}\] | \[\frac {BH^2}{24}\] | \[\frac {BH^3}{36}\] |
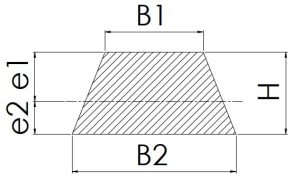 |
\[\scriptsize e1=\frac {(3B_1+2B_2)}{(2B_1+B_2)}×\frac {H}{3}\]\[\scriptsize e2=H-e1\] | \[\scriptsize (2B_1+B_2)×\frac{H}{2}\] | \[\scriptsize \frac{{6B_1}^2+6B_1B_2+{B_2}^2}{12×(3B_1+2B_2)}×H^2\] | \[\scriptsize \frac{({6B_1}^2+6B_1B_2+{B_2}^2)}{36×(2B_1+2B_2)}×H^2\] |
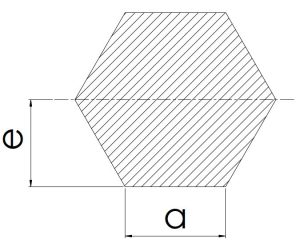 |
\[0.866a\]\[(\frac{\sqrt{3}}{2}×a)\] | \[2.598a^2\]\[(\frac{3\sqrt{3}}{2}×a^2)\] | \[\frac{5}{8}×a^3\] | \[0.5413a^4\]\[(\frac{5\sqrt{3}}{16}×a^4)\] |
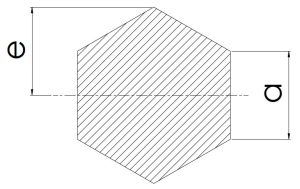 |
\[a\] | \[2.598a^2\]\[(\frac{3\sqrt{3}}{2}×a^2)\] | \[0.5413a^3\]\[(\frac{5\sqrt{3}}{16}×a^3)\] | \[0.5413a^4\]\[(\frac{5\sqrt{3}}{16}×a^4)\] |
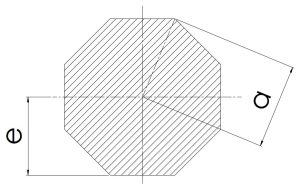 |
\[0.924a\] | \[2.828a^2\] | 0.6906 | \[0.5413a^4\]\[(\frac{5\sqrt{3}}{16}×a^4)\] |
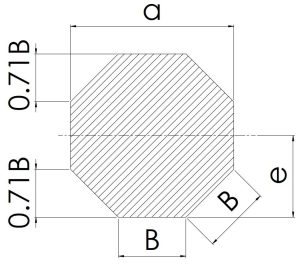 |
\[0.4142a\]\[\frac{a}{1+\sqrt{2}}\] | \[2.828a^2\] | 0.1095 | 0.0547 |
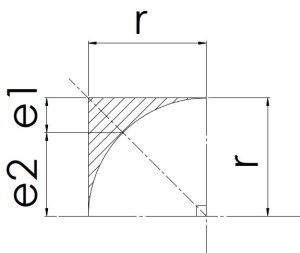 |
e1=0.2234r e2=0.7766r |
\[r^2(1-\frac{π}{4})\] | \[0.00966r^3\]\[(\frac{r^4}{e2}×0.0075)\] | \[0.0075r^4\] |
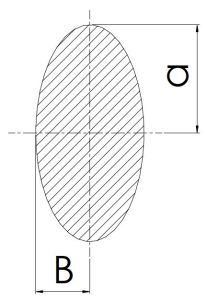 |
a | πBa | \[\frac{π}{4}Ba^3\] | \[\frac{π}{4}Ba^2\] |
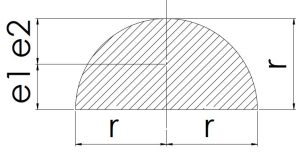 |
\[e1=0.4244r\]\[e2=0.5756r\] | \[\frac{πr^2}{2}\] | \[z1=0.2587r^3\]\[z2=0.1908r^3\] | \[(\frac{π}{8}-\frac{8}{9π})×r^4\] |
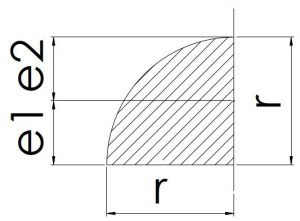 |
\[e1=0.4244r\]\[e2=0.5756r\] | \[\frac{πr^2}{4}\] | \[z1=0.1296r^3\]\[z2=0.0956r^3\] | \[0.055r^4\] |
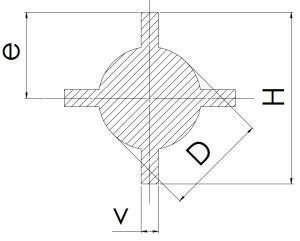 |
\[\frac{H}{2}\] | \[2v(H-D)+\frac{πd^2}{4}\] | \[\scriptsize \frac{1}{12}×{\frac{3π}{16}D^4\]\[\scriptsize +v(H^3-D^3)\]\[\scriptsize +v^3(H-D)}\] | \[\scriptsize \frac{1}{6H}×{\frac{3π}{16}D^4\]\[\scriptsize +v(H^3-D^3)\]\[\scriptsize +v^3(H-D)}\] |
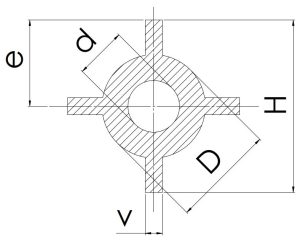 |
\[\frac{H}{2}\] | \[\scriptsize 2v(H-d)+\frac{π(D^2-d^2)}{4}\] | \[\frac{2×H}{3}\] | \[\frac{2×H}{3}\] |
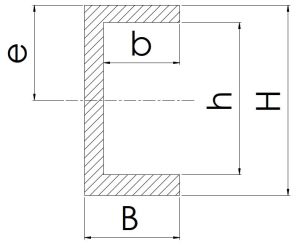 |
\[\frac{H}{2}\] | \[HB-hb\] | \[\frac{BH^3-bh^3}{6H}\] | \[\frac{BH^3-bh^3}{12}\] |
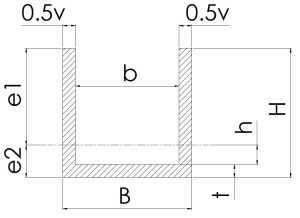 |
\[e1=H-e1\]\[\scriptsize e2=\frac{(vH^2+bt^2)}{(vH+bt)}×\frac{1}{2}\] | \[\scriptsize HB-b(e2+h)\] | \[z1=\frac{i}{e1}\]\[z2=\frac{i}{e2}\] | \[\scriptsize \frac{Be1^2-bh^3+ve2^3}{3}\] |
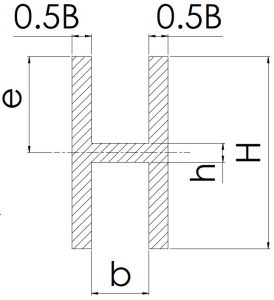 |
\[\frac{H}{2}\] | \[HB+hb\] | \[\frac{BH^3+bh^3}{6H}\] | \[\frac{BH^3+bh^3}{12}\] |
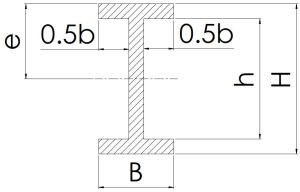 |
\[\frac{H}{2}\] | \[HB-hb\] | \[\frac{BH^3-bh^3}{6H}\] | \[\frac{BH^3-bh^3}{12}\] |
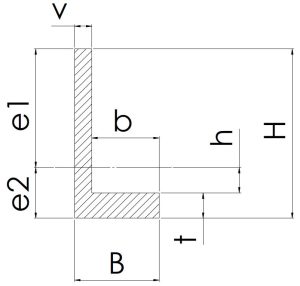 |
\[e1=H-e1\]\[\scriptsize e2=\frac{vH^2-bt^2}{vH+bt}×\frac{1}{2}\] | \[HB-b(e2+h)\] | \[z1=\frac{i}{e1}\]\[z2=\frac{i}{e2}\] | \[\scriptsize \frac{Be1^2-bh^3+ve2^3}{3}\] |


